Bernoulli's Principle
Bernoulli's theorem is a principle that helps us understand how the speed of a fluid (like air or water) changes when it moves through different areas or along a pipe.
Imagine you have a hose, and you're holding your thumb over the opening to create a small opening for the water to flow out. When the opening is small, the water comes out with a higher speed. But when you remove your thumb and open the hose wider, the water comes out with a lower speed.
Bernoulli's theorem says that as the speed of a fluid increases, its pressure decreases, and vice versa. So, when the water flows through the narrow opening (at higher speed), the pressure decreases, and when it flows through the wider opening (at lower speed), the pressure increases.
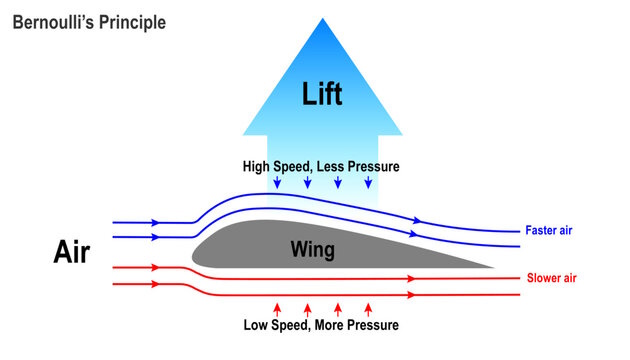
This principle is essential for understanding how things like airplanes generate lift, how sprinklers work, and even how the wind blows around buildings. It's a fundamental concept in fluid dynamics that helps explain the behavior of fluids in different situations.
In more technical terms, Bernoulli's theorem is a fundamental principle in fluid dynamics that describes the relationship between the pressure, velocity, and height of a fluid in steady flow. It is based on the concept of conservation of energy within the fluid system.
Mathematically, the theorem can be expressed as:
P + ½ ρ v^2 + ρ g h = constant
Where:
P is the pressure of the fluid at a particular point,
ρ is the density of the fluid,
v is the velocity of the fluid at that point,
g is the acceleration due to gravity,
h is the height of the fluid above a reference level,
and the sum of the terms (½ ρ v^2 + ρ g h) represents the dynamic pressure and the potential energy per unit volume, respectively.
In simpler words, as the fluid flows through a pipe or over an obstacle (like an airplane wing), its pressure decreases if the velocity increases, and vice versa. This is because the total energy of the fluid per unit volume remains constant along the flow path (assuming no energy is added or taken away from the system).
The theorem has wide applications in understanding various phenomena, including lift generation in wings, the behavior of fluids in pipes, the operation of turbines and pumps, and even weather patterns. While the concept is powerful and applicable in various engineering and scientific fields, its mathematical formulation can be quite complex and requires a solid understanding of fluid mechanics and calculus to fully grasp its intricacies.